Beyond Weisfeiler-Lehman: using substructures for provably expressive graph neural networks
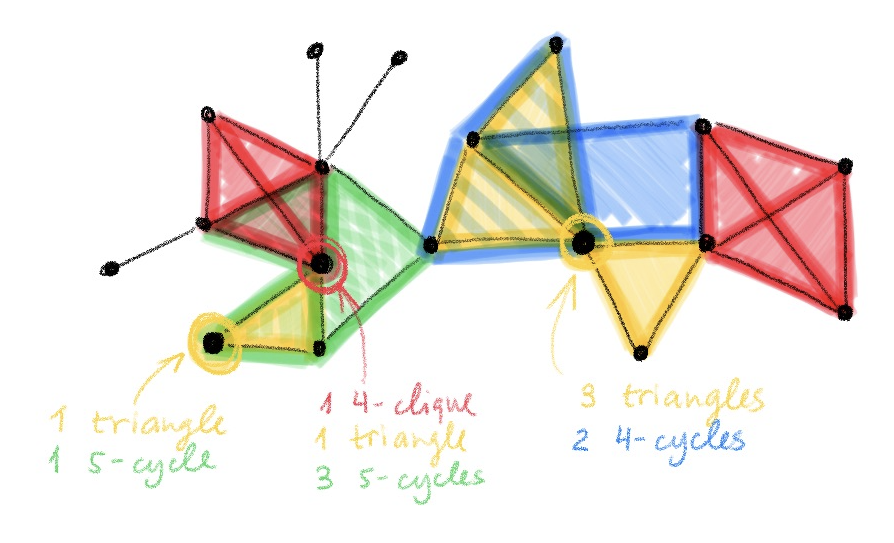
TL;DR: In this post, I discuss how to design local and computationally efficient provably powerful graph neural networks that are not based on the Weisfeiler-Lehman tests hierarchy. This is the second in the series of posts on the expressivity of graph neural networks.
---
See Part 1 describing the relation between graph neural networks and the Weisfeiler-Lehman graph isomorphism test. In Part 3, I will argue why we should abandon the graph isomorphism problem altogether.---
Recent groundbreaking papers[1–2] established the connection between graph neural networks and the graph isomorphism tests, observing the analogy between the message passing mechanism and the Weisfeiler-Lehman (WL) test[3]. WL test is a general name for a hierarchy of graph-theoretical polynomial-time iterative algorithms for determining graph isomorphism. The k-WL test recolours k-tuples of vertices of a graph at each step according to some neighbourhood aggregation rules and stops upon reaching a stable colouring. If the histograms of colours of the two graphs are not the same, the graphs are deemed not isomorphic; otherwise, the graphs are possibly (but not necessarily) isomorphic.
Message passing neural networks are at most as powerful as the 1-WL test (also known as node colour refinement), and thus unable to distinguish between even very simple instances of non-isomorphic graphs. For example, message passing neural networks cannot count triangles[4], a motif known to play an important role in social networks where it is associated with the clustering coefficient indicative of how “tightly knit” the users are[5]. It is possible to design more expressive graph neural networks that replicate the increasingly more powerful k-WL tests[2,6]. However, such architectures result in high complexity and large number of parameters, but most importantly, typically require non-local operations that make them impractical.
---
Examples of non-isomorphic graphs that cannot be distinguished by 1-WL but can be distinguished by 3-WL due to its capability of counting triangles.
Thus, provably powerful graph neural networks based on the Weisfeiler-Lehman hierarchy are either not very powerful but practical, or powerful but impractical[7]. I argue that there is a different simple way to design efficient and provably powerful graph neural networks, which we proposed in a new paper with Giorgos Bouritsas and Fabrizio Frasca[8].
Graph substructure networks
The idea is actually very simple and conceptually similar to positional encoding or graphlet descriptors[9]: we make the message passing mechanism aware of the local graph structure, allowing for computing messages differently depending on the topological relationship between the endpoint nodes. This is done by passing to message passing functions additional structural descriptors associated with each node[10], which are constructed by subgraph isomorphism counting. In this way, we can partition the nodes of the graph into different equivalence classes reflecting topological characteristics that are shared both between nodes in each graph individually and across different graphs.
We call this architecture graph substructure network (GSN). It has the same algorithmic design and memory and computational complexity as standard message passing neural networks, with an additional pre-computation step in which the structural descriptors are constructed. The choice of the substructures to count is crucial both to the expressive power of GSNs and the computational complexity of the pre-computation step.
The worst-case complexity of counting substructures of size k in a graph with n nodes is O(nᵏ). Thus, it is similar to high-order graph neural network models or Morris[2] and Maron[6]. However, GSN has several advantages over these methods. First, for some types of substructures such as paths and cycles the counting can be done with significantly lower complexity. Secondly, the computationally expensive step is done only once as preprocessing and thus does not affect network training and inference that remain linear, the same way as in message-passing neural networks. The memory complexity in training and inference is linear as well. Thirdly and most importantly, the expressive power of GSN is different from k-WL tests and in some cases is stronger.
How powerful are GSNs?
The substructure counting endows GSN with more expressive power than the standard message-passing neural networks. First, it is important to clarify that the expressive power of GSN depends on the graph substructures used. Same way as we have a hierarchy of k-WL tests, we might have different variants of GSNs based on counting one or more structures. Using structures more complex than star graphs, GSNs can be made strictly more powerful than 1-WL (or the equivalent 2-WL) and thus also more powerful than standard message passing architectures. With 4-cliques, GSN is at least no less powerful than 3-WL, as shown by the following example of strongly regular graphs on which GSN succeeds while 3-WL fails:
---
Example of non-isomorphic strongly regular graphs with 16 vertices and node degree 6, where every two adjacent vertices have 2 mutual neighbours, and every two non-adjacent vertices also have 2 mutual neighbours. The 3-WL test fails on this example, while GSN with 4-clique structure can distinguish between them. In the graph on the left (known as the Rook’s graph) each node participates in exactly one 4-clique. The graph on the right (Shrikhande graph) has maximum cliques of size 3 (triangles). Figure from[8].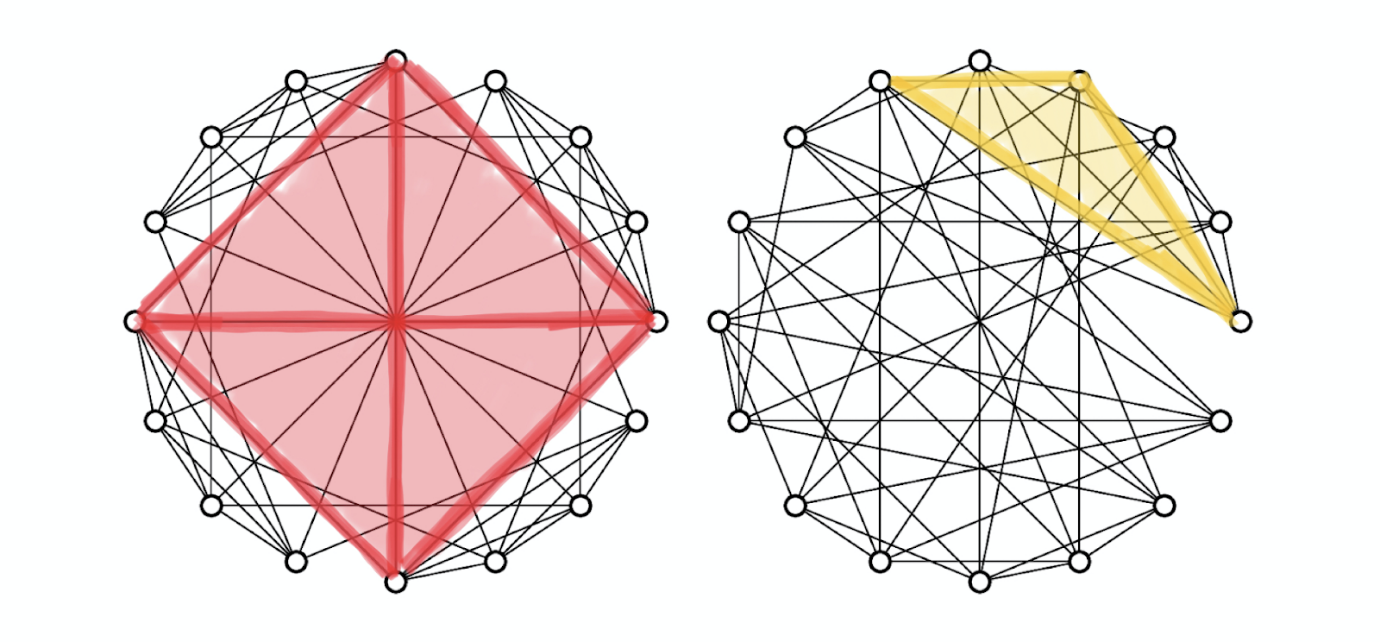
More generally speaking, for various substructures of O(1) size, as long as they cannot be counted by 3-WL, there exist graphs where GSN succeeds and 3-WL fails[11]. While we could not find examples to the contrary, they might in principle exist — that is why our statement about the power of GSN is of a weak form, “at least not less powerful”.
This holds for larger k as well; a generalisation of strongly regular graphs in the above figure, called k-isoregular, are instances on which the (k+1)-WL test fails[12]. These examples can also be distinguished by GSN with appropriate structures. The expressive power of GSNs can thus be captured by the following figure:
---
GSN is outside the Weisfeiler-Lehman hierarchy. With the appropriate structure (e.g. cliques or cycles of certain size), it is likely to be made at least not less powerful than k-WL.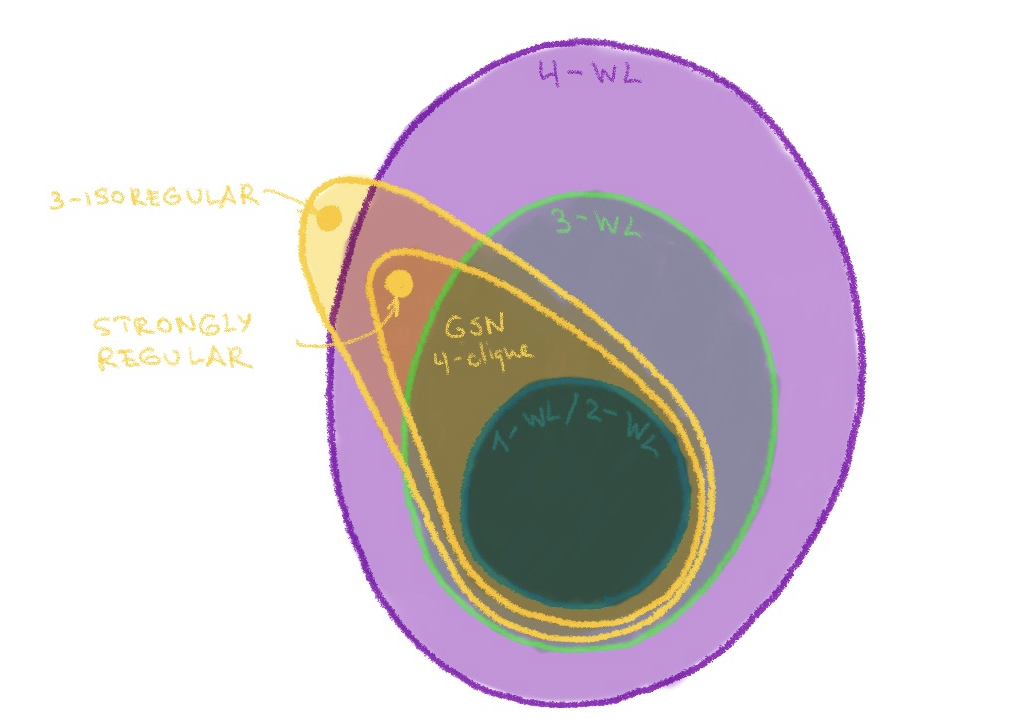
How powerful can GSN be in principle? This is still an open question. The graph reconstruction conjecture[13] postulates the possibility of recovering a graph from all its node-deleted substructures. Thus, if the reconstruction conjecture is correct, a GSN with substructures of size n−1 would be able to correctly test isomorphism of any graphs. However, the reconstruction conjecture is currently proven only for graphs of size n≤11[14], and second, such large structures would be impractical.
The more interesting question is whether a similar result exists for “small” structures (of O(1) size independent of the number of nodes n). Our empirical results show that GSN with small substructures such as cycles, paths, and cliques work for strongly regular graphs, which are known to be a tough nut for the Weisfeiler-Lehman tests.
Most importantly, GSN builds on top of standard message-passing architectures and thus inherits its locality and linear complexity. The hyperparameters of the method include the structures counted for the construction of the structural descriptors. It is likely that practical applications will be guided by the tradeoff between the required expressive power, the size of the structures that can guarantee it, and the complexity of computing them.
---
Using GSN with cycles of length k≥6 significantly improves the prediction of chemical properties of molecular graphs in the ZINC database that is used by pharmaceutical companies for virtual screening of drug candidates. Such cyclic structures are abundant in organic molecules. Figure from[8].
In our experiments, we observed that different problems and datasets benefit from different substructures, so it is likely that this choice is problem-specific. Fortunately, we often know what substructures matter in some applications. For example, in social networks, triangles and higher-order cliques are common and have a clear “sociological” interpretation. In chemistry, cycles are a very frequent pattern, such as 5- and 6-membered aromatic ring that appear in a plethora of organic molecules. The figure below shows an example most of us are familiar with, the molecule of caffeine, whose level in my bloodstream is alarmingly low. This sounds like the right moment to finish this post and make myself a cup of coffee.
---
1,3,7-Trimethylxanthine, better known as caffeine, is an example of a chemical cyclic compound containing 5- and 6-rings (denoted by red and yellow).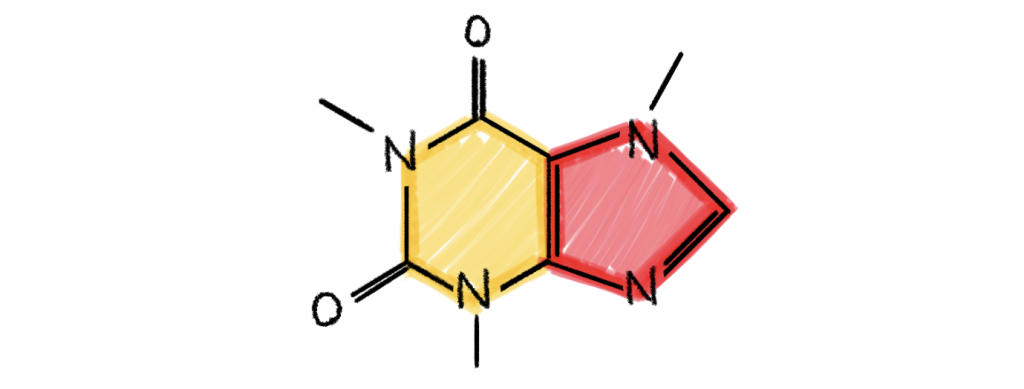
Notes and references
[1] K. Xu et al. How powerful are graph neural networks? (2019). Proc. ICLR.
[2] C. Morris et al. Weisfeiler and Leman go neural: Higher-order graph neural networks (2019). Proc. AAAI.
[3] B. Weisfeiler, A. Lehman, The reduction of a graph to canonical form and the algebra which appears therein, 1968 (English translation)
[4] Consequently, two graphs with a different number of triangles would be considered possibly isomorphic by the 1-WL test, or equivalently, will have an identical embedding constructed by a message passing neural network. There have been substantial new results extending our understanding of what structures are invariant under WL tests, see e.g. V. Arvind et al. On Weisfeiler-Leman invariance: subgraph counts and related graph properties (2018) arXiv:1811.04801 and Z. Chen et al. Can graph neural networks count substructures? (2020) arXiv:2002.04025.
[5] Graph substructures have been used in complex networks for decades now. In bioinformatics, the seminal papers of R. Milo et al. Network motifs: simple building blocks of complex networks (2002). Science 298 (5594):824–827. and N. Pržulj et al. Modeling Interactome: Scale-free or geometric? (2004) Bioinformatics 20(18):3508–3515 introduced graph motifs and graphlets for the analysis of biological interaction networks. In social networks, the study of triangular motifs dates back to at least P. W. Holland and S. Leinhardt, Local structure in social networks (1976). Sociol. Methodol. 1–45.
[6] H. Maron et al. Provably powerful graph neural networks (2019). Proc. NeurIPS.
[7] The 3-WL-equivalent graph neural network architecture of Morris has O(n³) space – and O(n⁴) time complexity. The architecture of Maron has a slightly better O(n²) space – and O(n³) time complexity. For a modestly-sized graph with 1M nodes this still translates into enormous 1TB of memory and an exaflop of computation.
[8] G. Bouritsas et al. Improving graph neural network expressivity via subgraph isomorphism counting (2020). arXiv:2006.09252.
[9] Graph analysis approaches based on substructure counting obviously predate the recent works on graph deep learning. Notable examples include the graphlet signatures proposed in bioinformatics in T. Milenkoviæ and N. Pržulj, Uncovering biological network function via graphlet degree signatures (2008). Cancer Inform. 6:257–273, or graphlet kernels N. Shervashidze et al. Efficient graphlet kernels for large graph comparison (2009). Proc. AISTATS.
[10] We show the same mechanism for edges as well, which I omit here for brevity.
[11] 3-WL appears to be rather weak in terms of substructure counting. For example, it can count motif cycles of up to 7 nodes, but fails to count induced 4-cycles or paths of length 4. It is currently not clear what substructure counting capabilities are obtained by going up in the WL-hierarchy.
[12] B. L. Douglas, The Weisfeiler-Lehman method and graph isomorphism testing (2011). arXiv:1101.5211. Note that there is some level of confusion between what different references call “k-WL”. Douglas uses the term k-WL for what others call (k−1)-FWL (“folklore” WL). In our terminology, k-WL fails on (k−1)-isoregular graphs. Strongly regular graphs are 2-isoregular.
[13] P.J. Kelly, A congruence theorem for trees (1957). Pacific J. Math. 7:961–968.
[14] B. D. McKay, Small graphs are reconstructible (1997). Australasian J. Combinatorics 15:123–126.
Acknowledgements
I am grateful to Luca Belli, Giorgos Bouritsas, and Fabrizio Frasca for their help with proof-reading this post. See other posts on Graph Deep Learning.
This article was originally published on Towards Data Science.