Can FX hedges of bonds deliver a free lunch?

We all know that in the markets, there is no such thing as a free lunch. Risk-free returns don’t exist – and if they did, even briefly, they would be traded on until they disappeared. Except sometimes, somehow, under just the right circumstances, the elusive free lunch may temporarily appear on the table… In this article, Jessica James, Managing Director, Senior Quant Researcher, Commerzbank, explores how.

I would like to talk about government bond yield differentials. At the time of writing, US 2y government bonds deliver about 1.5%. Similar EU bonds are giving -0.6%. Investors in high grade debt based in Europe are enviously glancing over the pond.

Why don’t they sell some EU bonds and buy the US bonds? Ah, says your Finance 101 lecturer, because of the FX risk. If a EUR based investor buys a US bond, the FX rates can swing by several percent in a few days or weeks – wiping out the carefully calculated interest rate differential. The FX risk overwhelms the trade.

Well then, why does the investor not hedge the FX risk of the trade? Once more, the Finance 101 lecture notes have an answer – because the cost of hedging will exactly offset the interest rate differential. So our investor sadly regards his underperforming portfolio and wonders what to do. But! His notes are from pre 2008 days – and these days, things are a little different. The FX hedge in the post crisis world is affected by the cross currency basis, which means that sometimes, the FX hedged deal is a lot more interesting.

(For an in-depth discussion of what the basis is, see Commerzbank’s Rates Radar “More interest in cross-currency basis swaps”, March 2017.)

Maturity-matched hedges

As a EUR based investor, the higher yields currently available for US bonds across the tenor range are attractive. How could the EUR based investor take advantage of this?

In a financial market with no capital charges or regulatory and XVA issues, then it would not be possible to preserve any kind of yield pick-up by investing in a foreign bond and then hedging the FX risk. The ‘theoretical’ forward FX rate would, in the pre-2008 crisis days, have almost exactly cancelled out the yield pick-up, though there might have been some credit spread available. But even this was small.

Now, however, there exists in general a substantial cross-currency basis, meaning that the arbitrage relationship between FX spot and forward, and interest rates, has broken down to an extent, due partly to demand for different currencies and partly to regulatory activity which restricts arbitrage trades. The actual cross currency basis is usually expressed as a difference to the non-USD interest rate of the currency pair, though it could equally well be expressed as a spread to the USD rate or to the FX spot or theoretical forward rate. Additionally, credit spread differentials have become far more significant since the crisis, and may provide additional pick-up in different industries and tenors.

We would execute the hedge in the swap market, which has slightly different rates from the government bonds (though they are correlated), and we would include the basis swap. The (US) basis swap is the extra cost of borrowing US dollars via a currency swap compared to what it should be purely according to interest rate differentials.

What, then, will the cost of hedging be? The mechanics of the package are thus: the EUR based investor exchanges EUR for USD, buys the USD bond, and puts on a maturity-matched FX hedge. Simplistically, assuming a 1-year period, and without worrying about coupon payments, we can write this as below.

FX is the FX rate at the start of the deal

FR₁ is the 1 year forward FX rate for the bond maturity

As said, we are not worrying about hedging the interest rate risk.

Thus

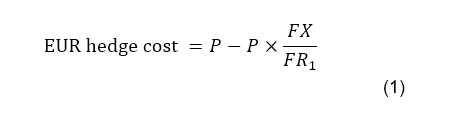
But from the arbitrage based construction of the forward rate FR, we know that

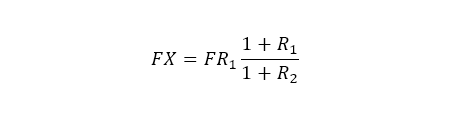
Where R₁ is the EUR interest rate, and R₂ is the USD interest rate for the bond tenor.

Thus EUR hedge cost is given by

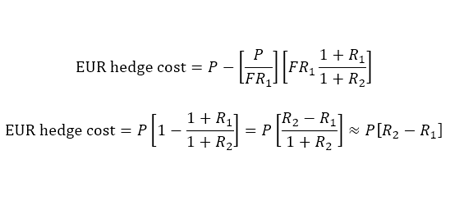
R₂ is the USD swap rate, but we actually now need to adjust it by the basis swap amount. Thus

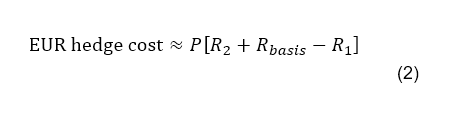
Because (1) and (2) are approximately equal to each other, it can be calculated either way, depending on the data which is available. One would usually use equation (2) as the basis swap is explicitly incorporated, but if one wished to use the spot and forward FX rates, then it is possible to express the quantity [R₂ + R_basis - R₁] in terms of these FX rates as in equation (1), because the forward FX rate in the market does incorporate the basis.

It’s not difficult to extend this to the multi-year case. We know that for n years,

So the total EUR hedge cost over the whole deal is given by

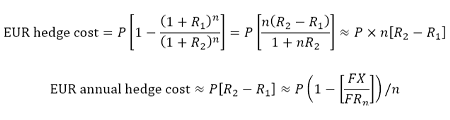
…if we use a binomial expansion and take only the first order. Once more of course we actually need to include the basis swap so the actual annual cost will be P[R₂ + R_basis - R₁].

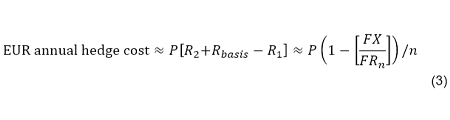
So we may now calculate a hedged yield pick-up which is actually accessible to the EUR based investor. It is FX hedged and relatively risk free. Note that equation (3), where the hedge cost is expressed in terms of the FX spot and forward rates, is a novel way of calculating hedge cost. It is useful in that it is an alternative way of arriving at the answer from other data series than those usually used.

Practical calculation of maturity-matched yield pick-up

From now on, we can omit the principal amount P in expressions as it will always cancel on both sides of the equation and there is no loss of generality in expressing all quantities as percentages.

Once we have the hedge cost, we may derive the annualised yield pick-up very simply, as below

As previously discussed, in a perfectly efficient market, this would be zero, but in the ‘real world’ it is often substantial.

In practice, we may derive this yield pick-up three ways

1. Using bond yields, swap rates, and cross-currency basis swaps
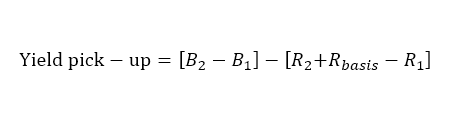
2. Using asset swap spreads, 3s6s basis swaps, and cross-currency basis swaps
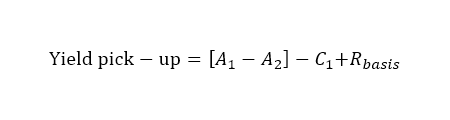
3. Using bond yields and spot and forward FX rates

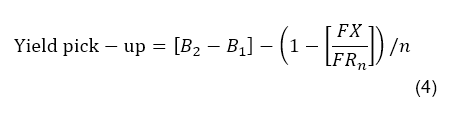
Where, for a EUR investor buying a USD government bond,

B₁ = EUR bond yield
B₂ = USD bond yield
R₁ = EUR swap rate
R₂ = USD swap rate
R_basis = XCCY basis swap
A₁ = EUR asset swap
A₂ = USD asset swap
C₁ = 3s6s basis
FX = spot foreign exchange rate
FR_n = forward foreign exchange rate for tenor n
n = tenor in years

Note that the 3s6s basis (ie., the difference between swap rates referenced to 3m and 6m Libor) may sometimes be needed if the other interest rates differ in their coupon frequency, and that the asset swap spread is A₁ - A₂ rather than A₂ - A₁ because it is always quoted as a positive spread over the government bond. Additionally, one may need to be careful of the sign of the basis swap which is usually quoted as a spread to the non-USD interest rate, so if the basis-adjusted EUR interest rate is lower than the actual rate, then the basis swap will be a negative number.

Having done all of this, we see in the graph below that the three ways of calculating the yield pick-up match beautifully!

---

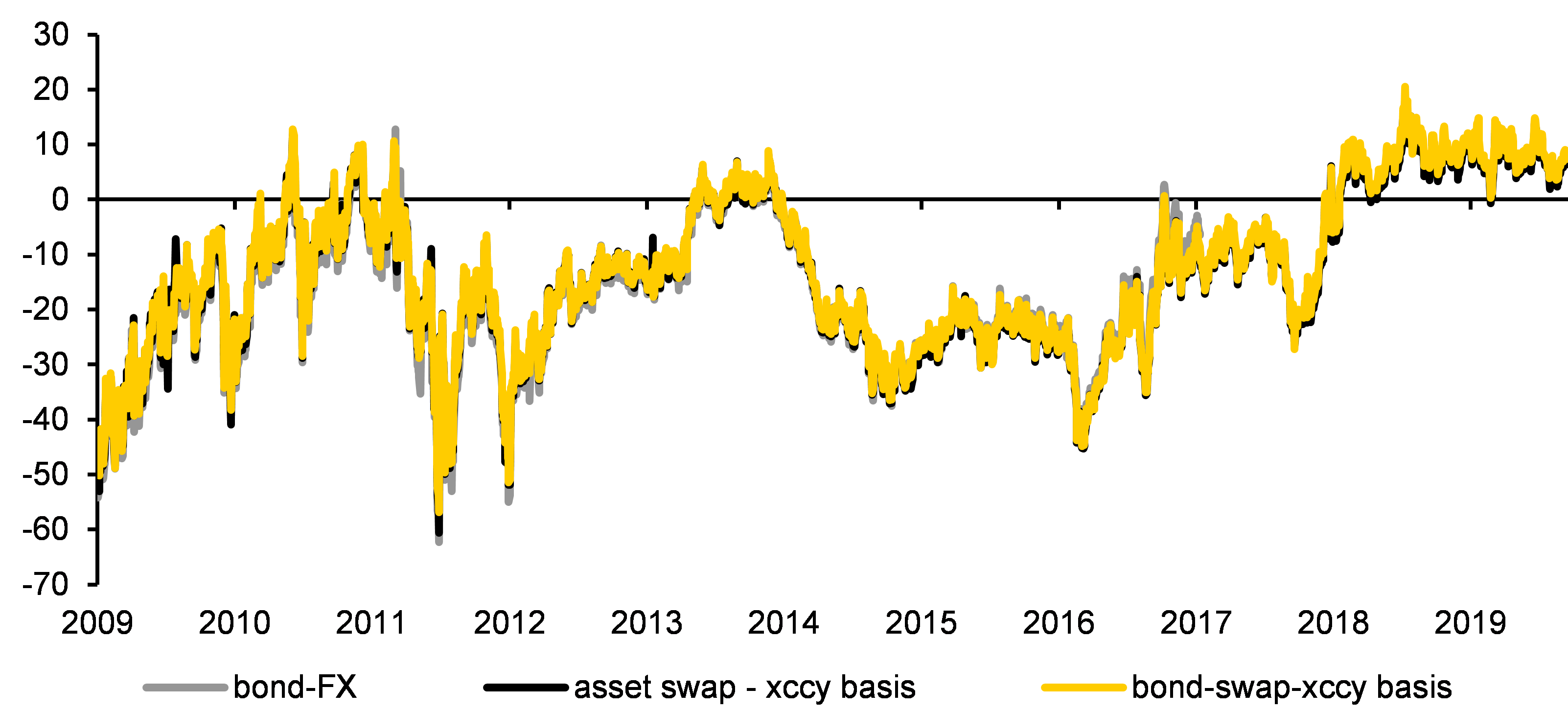
Source: Commerzbank Research, Bloomberg

---

It’s obvious that the ‘pick-up’ is not always positive – the point one can make is that a negative pick-up from the perspective of one currency of a pair is a positive one from the other currency’s perspective. But the fact that at times, certain investors have been able to lock in a pick-up of 50 bp or more does make one think that just occasionally, lunch comes without a bill.

Now, this is of course not the whole story. We’ve assumed that the investor can short EUR government bonds in the repo market without cost, which is not true. And these pickups are only strictly available if the investor holds the bonds until maturity – two years, in the above example. This does not suit the majority of portfolio managers. However, it is good to think that in today’s world, many of the old certainties which are no longer true give way to far more interesting situations.

This article was originally published in the QuantMinds eMagazine Innovations in quant trading strategies and modelling. Read the latest eMagazine >>

---