Faster, more accurate pricing using polynomial approximations

Expectations of discounted functions of stochastic processes are the bedrock of much of mathematical finance. European option prices, bond prices, spreads, and default risk all require the calculation of one or more expectations of functions of a stochastic process at some future time. The discounting is usually at the short rate, but can include hazard rate components when default or rating migration plays a role.
In some cases, these expectations have an analytical solution, such as the Black-Scholes option price and the price of a bond with Cox-Ingersoll-Ross short rate dynamics. In other cases, we need to rely on approximations and numerical techniques, such as binomial trees or PDE solvers. Shifted log-normal short rate models come to mind, as well as rating transition models. These techniques are often slow and imprecise, which is a problem especially in calibration and scenario generation, or in general when many price evaluations are required.
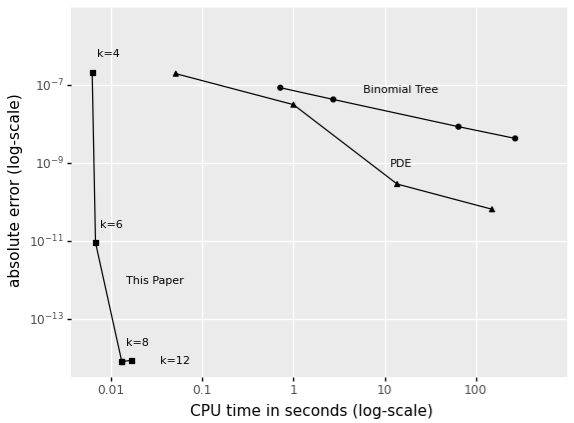
In Zhao, Van Beek, Spreij and Ba (2021) we introduce a fast and generic expansion of discounted moments of stochastic processes that is applicable to a wide array of pricing problems. On benchmark problems (where an analytical solution is known) we find our approach to be several orders of magnitude faster and more accurate than baseline implementations of binomial trees, PDEs and Monte-Carlo methods. Figure 1 below shows the computation time against the error for various numerical methods employed to price a CIR bond. Even with a low order (k) of the expansion, we quickly converge to a few orders above machine precision.
Figure 1: Comparison of different numerical approximations to the 10-year CIR bond yield, given standard parameter values. All approximations presented are naïve Python implementations, hence not optimized for speed or memory use.
Our approach relies on high-order polynomial approximation of discounted moments. Given some technical regularity conditions, we show that the moments of a process at maturity are determined by a polynomial basis of its state space (e.g. 1, x, x2, x3, … for univariate processes with the (half) real line as the state space), as well as an infinitely large matrix A derived from the infinitesimal generator. The approximation arises from projecting this matrix onto a finite number of dimensions, Ak. Effectively this means that the coefficients of the polynomial can be written as a simple function of the parameters of the process, and the horizon at which we need to calculate the moments. That is, the vector exp{tAk}ei holds all coefficients for moment i at horizon t. Discounting is added by modifying the infinitesimal generator appropriately. A more detailed description can be found in Zhao et al. (2021), along with a Python notebook.
Once we have the discounted moments for some order, say 20, we can very efficiently compute 20th order polynomials. A zero-coupon bond price is simply the discounted zero-th moment, and an option payoff function can be approximated by a polynomial. Moments can also be translated to cumulants, which can be used in expansions of option prices through Gram-Charlier distributions (Chateau & Dufresne, 2017). Conveniently, the coefficients of the polynomial do not depend on the state of the process. This means that they can be precalculated offline and applied to all scenarios in a scenario simulation. For a given parameterization of the process, on every path and in every scenario, only the powers of the process have to be calculated.
In Zhao et al. (2021) we demonstrate two applications. The first is pricing a zero-coupon bond of the Black-Karasinski type, i.e. the log-short rate follows an Ornstein-Uhlenbeck process. The second is a rating transition model in which the generator of the underlying continuous-time Markov chain is stochastic and driven by two processes, one for upgrades and one for downgrades. These two processes are jointly log-Ornstein-Uhlenbeck. This setup allows us to capture the empirical fact that upgrades tend to slow down as downgrades speed up in stressed markets.
Beyond these applications, we think our theory can be applied to introduce far richer stochastic dynamics in a broad range of pricing problems. Where previously analytical or semi-analytical solutions were almost a precursor to feasibility, the speed and accuracy gains from polynomial approximation can make more realistic dynamics possible.
Join Misha van Beek, Director, Blackrock, at QuantMinds International this December!
References
Chenyu Zhao, Misha van Beek, Peter Spreij, and Makhtar Ba. "Polynomial Approximation of Discounted Moments." arXiv preprint arXiv:2111.00274 (2021).
Chateau, Jean-Pierre, and Daniel Dufresne. "Gram-Charlier processes and applications to option pricing." Journal of Probability and Statistics 2017 (2017).
