From scarce to large data and back: machine learning in finance

The revolutionary success of artificial intelligence, nurtured by big data and superlative computer power, calls to be transferred to different areas. Fuelled by data, machine learning methods require an efficient handling of massively large datasets. Key to the successful transfer of machine learning methods to other fields is therefore the effective supply of large datasets. Here, we focus on adopting the prowess of deep learning to represent nonlinear multivariate financial data. This is a highly active research field with an exponentially growing literature, from which we here cite just a few, Han et al. (2017); H. Bühler et al. (2019); Becker et al. (2019); Bayer et al. (2019); Liu et al. (2019).
Schematically, we aim to learn multivariate nonlinear dependence of data with a deep neural network approach:
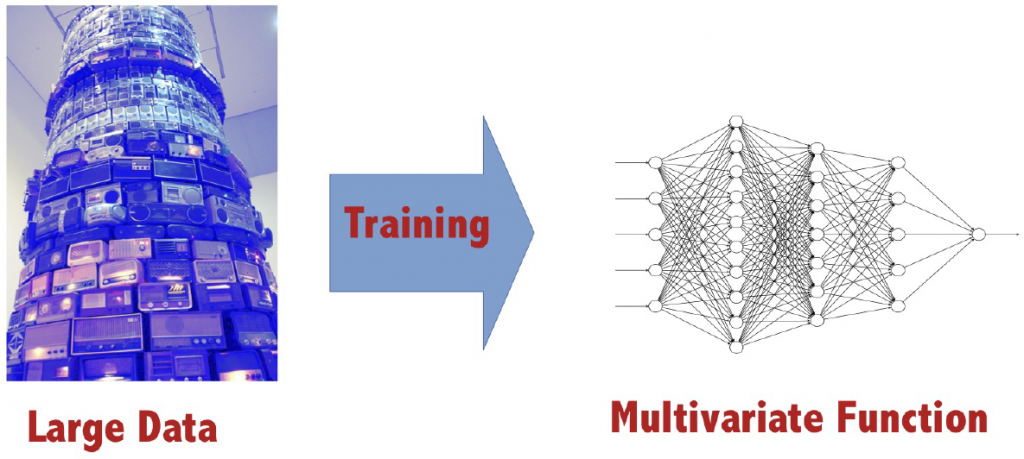
One commonly observed feature when training a neural network is that this is a data-hungry process. For our purpose, learning nonlinear functional relations from multivariate financial datasets, this evokes two main challenges.
Our first one is a large data challenge. It relates to at least two out of the big V’s of big data, namely volume and variety. We have to deal with datasets of utterly large sizes, and the data is of different types. Here, we are specifically interested in how to effectively store and process large multiway data sets. This means that we are interested in data that represents different types, and where the types can be interpreted as dimensions.
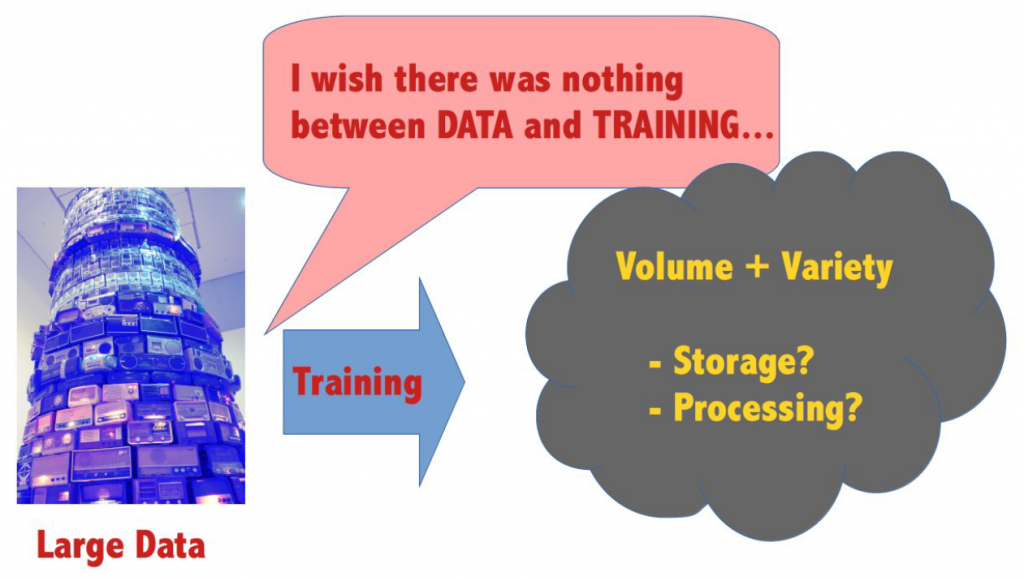
Our second challenge is, maybe surprisingly, virtually the opposite of the first one. It is a lack of large data challenge. In areas such as image recognition and natural language processing, thanks to an abundance of data, the required amount of data to feed machine learning methods in the training phase commonly is available. In finance, availability of price data highly varies over the different markets, with a range spanning from high frequency trading to over-the counter trading of structured products. For internal risk modeling, the core of the training data may stem from own trades, which may be rare. Even if data is flowing in high frequency, its use as training data is questionable, as financial data typically is non-stationary. The small data problem in finance has been tackled in Bühler et al. (2020), who present a data generator for financial time series. Here, we take a different perspective. Our aim is to effectively extrapolate multivariate financial data from a scarce sample.

To tackle these challenges, we first deepen our understanding of the structure and nature of the data under consideration. What sort of data do we want to represent by multivariate functions? In principle, we are aiming at learning multivariate relations of observed features to relevant financial quantities. The observed features may comprise classical financial data such as prices, trade volumes, credit ratings, interest rates, as well as alternative data such as news, memes, pictures, videos and any other state of the world that is considered relevant. In a classical financial model, all these features are represented in the guise of model parameters. The financially relevant output of the function, may be a fair option price, its sensitivities, the optimal exercise time, the value-at risk, etc.
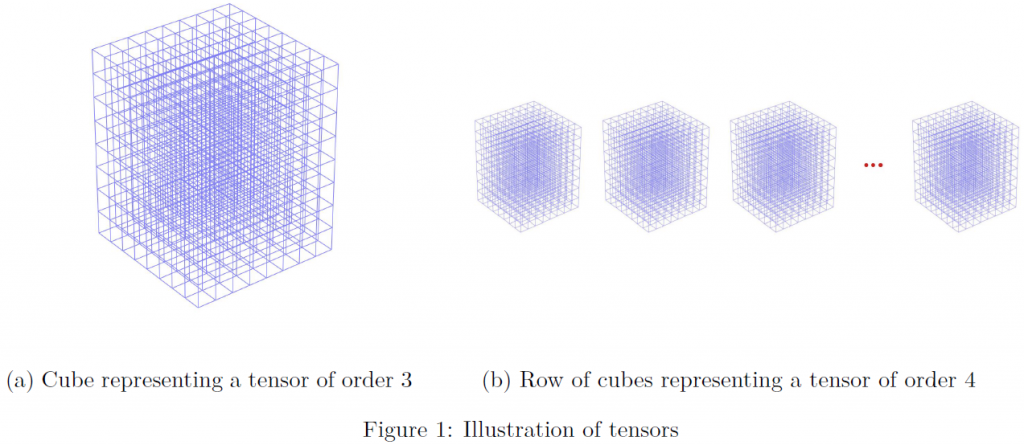
Let us turn to a concrete model example. We wish to learn the functional relation of the inputs, which are the spot price, volatility, time to maturity, strike and spot interest rate to the output, which is a fair price of an American option. One natural way to represent discrete multivariate functional data, is arranging them in a multidimensional array, i.e. as a tensor. In this example, we would have tensor of order 5. Figure 1 shows a schematical representation of tensors of order 3 and 4. When calculating or observing some price samples, this means that we observe the tensor only partially.
In order to cope with the tensor nature of our problem, we employ state-of-the-art tensor techniques. Multivariate data is omnipresent and in spotlight today in science, engineering, medicine, social sciences etc. Tensor techniques boost classical machine learning in multivariate settings. Therefore it is of little surprise that the field of tensor techniques and its applications is one of superlative growth, see for instance the survey articles Grasedyck et al. (2013); Ji et al. (2019).
To be more specific, we employ a tensor completion method tailored to extrapolate scarce data. In turn, tensor completion is also a versatile tool to compress large tensors, even if their sheer size does not allow us to access all individual entries. Tensor completion is a strikingly active part of tensor method research and application, as evidenced for instance by the recent survey article Song et al. (2019). Here, we employ the method from Glau et al. (2020) which builds on the low-rank tensor completion developed in Steinlechner (2016); Kressner et al. (2014).
For more details visit the session on Wednesday, and the preprint Colusso and Glau (2020) will be put online in the next couple of days.
References
Bayer, C., B. Horvath, A. Muguruza, B. Stemper, and M. Tomas (2019). On deep calibration of (rough) stochastic volatility models. preprint on arXiv:1908.08806v1.
Becker, S., Cheridito, and A. Jentzen (2019). Deep optimal stopping. Journal of Machine Learning Research 20.
Bühler, H., B. Horvath, T. Lyons, I. Perez Arribas, and B. Wood (2020). A data-driven market simulator for small data environments. http://dx.doi.org/10.2139/ssrn.3632431.
Colusso, P. and K. Glau (2020). Learning from multivariate data in finance with tensor completion: From scarce to large data and back. working paper.
Glau, K., D. Kressner, and F. Statti (2020). Low-rank tensor approximation for Chebyshev interpolation in parametric option pricing. SIAM Journal of Fiancial Mathematics 11 (3), 897–927. preprint version availbale under arXiv:1902.04367.
Grasedyck, L., D. Kressner, and C. Tobler (2013). A literature survey of low-rank tensor approximation techniques. GAMM-Mitt. 36 (1), 53–78.
H. Bühler, H., L. Gonon, J. Teichmann, and B. Wood (2019). Deep hedging. 19 (8), 1271–1291.
Han, J., J. A., and W. E (2017). Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences. accepted for publication.
Ji, Y., Q. Wang, X. Li, and J. Liu (2019). A survey on tensor techniques and applications in machine learning. IEEE Access 7, 162950–162990.
Kressner, D., M. Steinlechner, and B. Vandereycken (2014). Low-rank tensor completion by Riemannian optimization. BIT 54 (2), 447–468.
Liu, S., C. Oosterlee, and S. Bohte (2019). Pricing options and computing implied volatilities using neural networks. Risks 7 (16).
Song, Q., H. Ge, J. Caverlee, and X. Hu (2019). Tensor completion algorithms in big data analytics. ACM Trans. Knowl. Discov. Data 13 (1), 6:1–6:42.
Steinlechner, M. (2016). Riemannian optimization for high-dimensional tensor completion. SIAM Journal on Scientific Computing 38 (5), S461–S484.