In Memoriam: Generalizations of the Carr-Madan spanning formula

The Carr and Madan (1998) spanning formula is possibly the most famous result championed by Peter Carr, with far-reaching impact on the financial industry—most visibly the VIX—as well as academic research. This talk proposes to honor Peter’s legacy by expounding the formula in connection with related results, and presenting recent generalizations obtained under his broad guidance, with particular focus on multi-asset European options.

Specifically, the Carr and Madan formula decomposes the payoff f(S) of an arbitray European option as a combination of cash, underlying asset S, and a continuum of vanilla call and put options as:

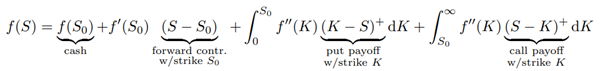
where S is the underlying asset terminal price, S₀ is an arbitrary split level (typically the spot or forward price), and t ⁺ := max(0, t) is the positive part of the number t. By the law of one price, the non-vanilla European option price f₀ is then uniquely determined by vanilla option prices[1] for any strike in a model-free fashion. Splendidly enough, the log-contract f(S) := ln S introduced by Neuberger (1990) can thus be priced and hedged with vanilla options—a key result used by Peter and others to devise an effective trading strategy for the replication of variance swaps, and adopted by CBOE in 2002 for the calculation of the VIX (2009).

The first generalization (Bossu, Carr, and Papanicolaou, 2021) uses functional analysis and integral equation theory to explore similar decompositions with “replicant” options other than vanillas, such as straddles and butterflies:

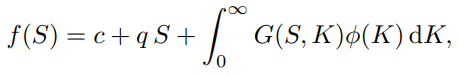
where G(S, K) is the known kernel of replicant option payoffs (e.g. G(S, K) := |S−K| for replication with straddles) and c, q, ϕ(K) are unknown quantities of cash and underlying asset to be determined. Formally, under mild conditions, ϕ(K) can be found by inverting the integral operator G induced by the replicant kernel G(S, K); that is, ϕ = G ⁻¹f. We show how this inversion may be done for the straddle kernel by spectral decomposition, with interesting truncation properties for fast pricing of vanilla options.

The second generalization (Bossu, Carr, and Papanicolaou, 2022, and Bossu, 2022) explores the case of multi-asset European options with arbitrary payoff f(x₁, · · · , x_n) to be decomposed with vanilla basket calls with payoff (w₁x₁ + · · · + w_nx_n − k) ⁺ where x₁, . . . , x_n are the prices or returns of n underlying assets, w₁x₁ + · · · + w_nx_n is the basket price (portfolio return), and k is a fixed basket “strike” level. For two assets we want to find basket call quantities ϕ(w₁, w₂) such that

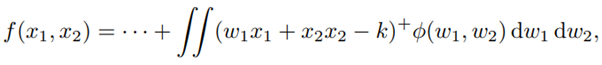
and more generally for n assets. We show how this replication problem can be solved for two classes of multi-asset options of interest: “standard” dispersion options with a payoff f(|x|) that is based on the Euclidean norm of the vector of asset performances, and the broader class of multi-asset European options with absolutely homogeneous payoff f(x; k). For the latter class, the solution is formally given as

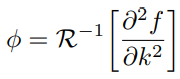
where R⁻¹ is the inverse Radon transform operator, an integral transform related to the Fourier transform which is used in medical imaging and other engineering applications. In particular, we derive first-time explicit decompositions for the dispersion call and put options, and for the two-asset best-of and worst-of call and put options. A novel generalization of the Breeden and Litzenberger (1978) formula for the multivariate implied distribution is also obtained.

References

Bossu, Sebastien (2022). “Static Replication of European Multi-Asset Options with Homogeneous Payoff”. In: Applied Mathematical Finance, pp. 1–14.

Bossu, Sebastien, Peter Carr, and Andrew Papanicolaou (2021). “A functional analysis approach to the static replication of European options”. In: Quantitative Finance 21 (4), pp. 637–655.

— (2022). “Static replication of European standard dispersion options”. In: Quantitative Finance 22.5, pp. 799–811.

Breeden, Douglas T. and Robert H. Litzenberger (1978). “Prices of state-contingent claims implicit in option prices”. In: Journal of business, pp. 621–651.

Carr, Peter and Dilip Madan (1998). “Towards a theory of volatility trading”. In: Volatility: New estimation techniques for pricing derivatives. Ed. by Robert A. Jarrow. Vol. 29. Risk books, pp. 417–427.

Neuberger, Anthony (1990). Volatility trading. Working paper. London Business School.

The CBOE volatility index—VIX (2009). Tech. rep. Chicago Board Options Exchange.

Footnote

[1] By put-call parity, the price of the forward contract is implied from vanilla option prices