Market-making for illiquid tokens: A challenge

What is the function of a market maker and what are the challenges of market making in illiquid digital markets? We answer these questions by presenting the theoretical foundations of an adaptive learning algorithm based on Bayesian inference. A real-world case study is presented, in which this knowledge is successfully applied.
The burgeoning digital asset ecosystem comprises many different participants. Token issuers, brokers, custodians, and digital exchanges, to name a few, are actively creating a novel decentralized vision of finance. In this new paradigm, a key role is played by market makers, providing the markets with vital liquidity. This service is a primary driver for a thriving and functioning digital asset ecosystem.
Many traditional financial institutions offering market-making services have been notoriously opaque about the details of the algorithms they utilize. However, modern scholarly literature on market making is founded on the study of market microstructure (Garman, 1976; Grossman and Miller, 1988). Some notable market-making models appeared in the 1980s (Ho and Stoll, 1981; Glosten and Milgrom, 1985; Kyle, 1985). These old-school theoretical foundations provided the fertile ground for modern algorithms to be developed upon, ones which are utilized in today's digital markets. One seminal incarnation, inspired by (Ho and Stoll, 1981), is the framework presented in (Avellaneda and Stoikov, 2008). Here, an optimal market-making strategy is described, which can be implemented in a limit order book of a liquid asset.
The problem of illiquidity
As the digital asset ecosystem continues to grow at an unstoppable rate, many newly emerging tokens are constrained by a stifling lack of liquidity. How, then, should a market-making algorithm be devised which can unlock illiquid tokens and nurture a mature market for them?
In general, the assumption underlying most market-making algorithms is the existence of a fair or true price. Bid and ask quotes are then placed around this invisible benchmark, depending on the current inventory, recent transactions, P&L expectations, and other constraints. In this context, the spread is a measure of the uncertainty related to the asset's true value. In other words, the challenge of market making is recast in an information-theoretic context. Specifically, there exists an information asymmetry between different market participants.
In (Glosten and Milgrom, 1985), this idea was formalised by the introduction of informed traders and noise traders. Then, (Das, 2005) extended this framework by maintaining a non-parametric probability density estimate of the asset's true value, which the market-maker algorithm utilises to compute bid and ask prices for the quotes. The algorithm essentially only needs to observe the transactions happening in the market as input. This feature of relying solely on the most minimal information available makes the framework an ideal tool for managing illiquid assets.
The key ingredient of the model is given by Bayesian inference. Before introducing some of the details of the model, a brief excursion into the history of probability is presented in the following.
Observing and updating
Most people get introduced to the concept of probability in the guise of its frequentist interpretation. In essence, this is the intuition that the result of a large number of trials will converge and reveal the nature of the underlying process. However, the revolution Thomas Bayes initiated is based on a simple question: “How should I modify my beliefs in the light of additional information?” In detail, the Bayesian interpretation assigns a probability to a hypothesis. At the core of the framework lies Bayes' famous theorem, updating the probability for the hypothesis as more evidence becomes available.
Today, Bayesian inference – the application of Bayes' theorem – is widely and successfully applied in science, engineering, medicine, and machine learning next to philosophy. Indeed, two scholars noted in the preface of their book on Bayesian epistemology, “Bayes is all the rage in philosophy” (Bovens et al., 2003). However, since its introduction in 1763, the theorem was mainly viewed as an obscurity at the fringes of mathematics. It perhaps would never have come to prominence were it not for a mathematician friend of Bayes and later the polymath Pierre-Simon Laplace, who both developed and extended the original ideas.
The mathematical engine
Following (Das, 2005), Vi denotes the true price of an asset at time ti and it is described by the probability density Ƥ(V = Vi). In other words, this is the prior probability reflecting the models belief about the true price. The market maker sets the bid and ask prices at which it is willing to buy and sell, respectively, at time ti. These are denoted by ![]()
α > 0 represents the proportion of informed traders in the market who know Vi and will always place orders if the true price is not inside the spread. Specifically, a buy order will be placed if ![]()
A sell order originates from a corresponding inverse condition. Consequently, (1 – α) describes the proportion of uniformed trades who place their buy and sell orders with a probability η Є |0, 0.5|, and thus no orders are placed with the probability (1 – 2η). Now, the unconditional probability for observing a trade can be expressed in terms of Ƥ(V = Vi), α,and η, and is called Ƥ (T), with the type T of the trade being a buy or a sell. In a similar way the (prior) conditional probabilities Ƥ (T|V = Vi) can be derived.
Every time the market maker observes a trade in the market, signalling information about the true value, the posterior probability is computed utilising Bayes' theorem
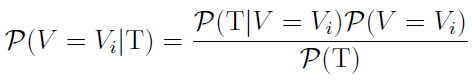
Expressed in words, Bayes's theorem states that the posterior probability is equal to the product of the prior probability Ƥ(V = Vi) of the true price and the conditional probability of the evidence given the hypothesis Ƥ (T|V = Vi), divided by the probability of new evidence becoming available Ƥ (T).
The expectation of the underlying value can be derived from the posterior conditional probability given the type of the observed order being T
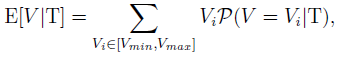
where the price range has been discretized and bounded by Vmin and Vmax. The zero-profit condition for the market maker is presented in (Glosten and Milgrom, 1985) and is given by setting
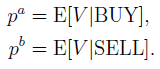
Technically, a mapping emerges
![]()
with the fixed point representing the zero-profit condition.
Adding more colour
The zero-profit spread represent an equilibrium from which the market maker will want to skew prices. This, however, is an art in itself. Depending on inventory sizes, P&L targets, expected price moves, to name a few variables, a market maker can asymmetrically skew the bid and ask prices of their quotes. This fine-tuning introduces feedback mechanisms leading to non-linear behaviour in the market. In essence, successful market making not only depends on formal constraints but is the result of a delicate mix containing additional creative considerations.
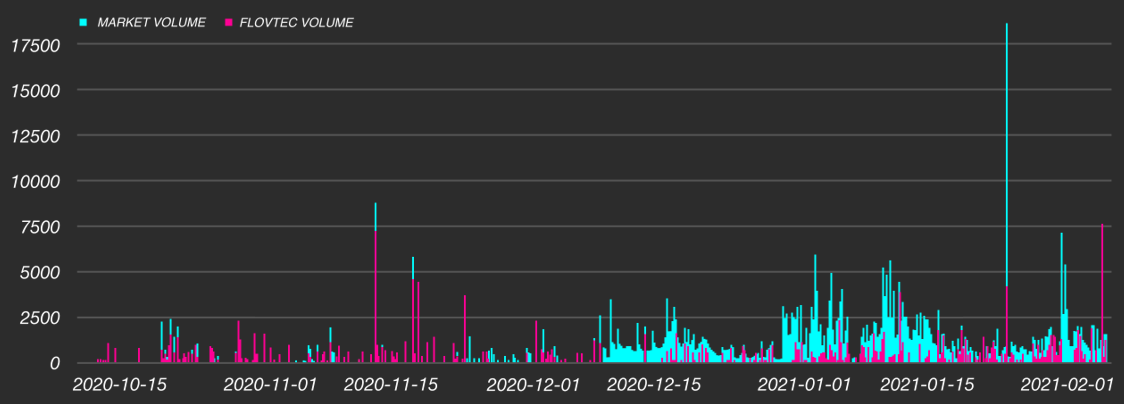
At flovtec, the resulting algorithm incorporating all the aforementioned elements is known as Octopus. Octopuses are perhaps the most famous cephalopods known for their highly adaptive behaviour. In Figure 1 a real-world case study is presented in which the Octopus algorithm transformed an illiquid token into a healthy and frequently traded digital asset in the time-span of two months. Specifically, within the first day of market making, the token's spread was reduced by a factor of 14, from 6.82% to 0.47%. The average traded volume of the token paired against USDT continuously increased. As a result, market participants noticed the newly emerging liquidity which enticed more traders to enter the market, establishing a positive feedback loop geared towards greater trading activity. In this way, flovtec is helping unlock the full potential inherent in a vibrant, prospering, and liquid digital assets ecosystem, token by token.
Figure 1: An illiquid token comes to life. Evolution of the traded volume over time, during which flovtec's market-making activities attracted more and more market participants.
References
Avellaneda, M. and Stoikov, S. (2008). High-frequency trading in a limit order book. Quantitative Finance, 8(3):217-224.
Bovens, L., Hartmann, S., et al. (2003). Bayesian epistemology. Clarendon Press, Oxford.
Das, S. (2005). A learning market-maker in the glisten-milgrom model. Quantitative Finance, 5(2):169-180.
Garman, M. B. (1976). Market microstructure. Journal of financial Economics, 3(3):257-275.
Glosten, L. R. and Milgrom, P. R. (1985). Bid, ask and transaction prices in a specialist market with heterogeneously informed traders. Journal of financial economics, 14(1):71-100.
Grossman, S. J. and Miller, M. H. (1988). Liquidity and market structure. the Journal of Finance, 43(3):617-633.
Ho, T. and Stoll, H. R. (1981). Optimal dealer pricing under transactions and return uncertainty. Journal of Financial economics, 9(1):47-73.
Kyle, A. S. (1985). Continuous auctions and insider trading. Econometrica: Journal of the Econometric Society, pages 1315-1335.
