Market risk: Optimal VaR adaptation & machine learning
Changing volatilities are constant companions in financial markets
time series. Nevertheless, regulatory risk models usually rely on some kind of stationarity assumption that leads to problems in these transient environments. Practitioners have long found some ad hoc solutions for this problem, but could machine learning lead to sustainable improvement?
Due to the pandemic, many banks experienced large numbers of backtest outliers in the first quarter of 2020 when they compared actual profit and loss numbers to VaR estimates. The simple reason was that their regulatory VaR systems were not able to adapt to rapidly changing market conditions as volatility spiked to ever-higher levels. The problem lies with the amount of data required to “train” the VaR system.
In a nutshell, the amount of training data is a compromise between having enough observations to compute relevant statistical quantities (here we want lots of data) and the degree to which this data is still relevant for the current environment (here we only want recent data). Whereas in quiet times collecting many data to reduce measurement uncertainty seems to be a priority in some model risk management approaches, the situation changes once there is a rapid shift as experienced in March 2020. Obviously, this may call for some mechanism to “learn” how to spot a crisis environment.
My talk at QuantMinds in Focus in May 2021 contained a simple approach using a noisy random walk, i.e. a stochastic process for which we have observations that include some additional disturbances. This lead to some very easy optimality criterion that depends on the Signal-to-Noise Ratio, the ratio between the variance of the innovation term and the variance of the disturbance term. That relatively simple approach yielded a quite good performance (see diagram) in tracking the profit and loss profile.
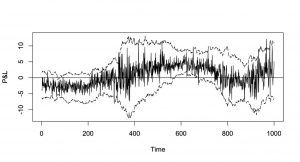
More details as well as additional Monte Carlo Studies can be found in the third edition of the book on Risk Model Validation by my colleague Christian Meyer and me (riskbooks.com).
Of course, that could only be a first step to improve classical regulatory VaR systems, since that approach does not care about other deficiencies (e.g. tail events). Are there any machine learning approaches that could be used to improve the situation?
The first technique that comes to mind is a Hidden Markov Chain, and indeed
the aforementioned noisy random walk is one of the simplest representatives of this kind. Hidden Markov Models have been around for quite a while. Their disadvantage of comparably large demands on computation time should not be too critical now. Nevertheless, in the context of market risk calculations, banks usually add market data from the current trading day and the algorithm should immediately integrate that information without re-running the lengthy calibration process. This calls for the usage of so-called online learning algorithms in contrast to batch learning approaches. Especially in the context of time series analysis, the sequential order of the data carries important information that should not be left out of the analysis.
What about methods based on neural networks? Even though there are quite a number of success stories e.g. in image / speech recognition, the application of neural networks in time series analysis seems to be quite limited. The first issue relates to the low signal-to-noise ratio usually encountered in financial market data. Due to the large noise component, the algorithm might learn the noise pattern, even though (at least in theory) there is nothing relevant to learn there. A clear indication of overfitting in this case is a good performance of the algorithm applied to the training data versus a deteriorating performance when applied to new data. Because of their complexity, neural networks are prone to overfit training data, i.e. they fit spurious random aspects of the training data, as well as structure that is true for the entire population. There are techniques to handle overfitting, and all machine learning developers should be making use of these techniques.
Finally, what are the main challenges when it comes to the application of machine learning in a regulatory context?
Explainability / interpretability: One should be in a position to explain how the algorithm makes a prediction or decision for one specific case at a time.
Robustness and transient environments: One should account for the fact that markets or environments can change, that calls for a good balance of adaptability and robustness.
Bias and adversarial attacks: Compared to classical statistics there is a much more prominent role for (training) data in machine learning applications.
Of course, some of these issues have been addressed within the machine learning community. What is needed now is the transfer to the banking industry without “reinventing the wheel”. For that reason, the Model Risk Managers’ International Association (mrmia.org) issued a white paper to discuss some (banking) industry best practices. That would only be a starting point since the applications are rapidly evolving.