Quantum machine learning with near-term quantum computing

Quantum computing is a growing and exciting field at the intersection of physics and computing. A quantum computer can solve certain types of problems exponentially faster than their classical counterparts, with long-term potential for impact in chemistry, biology and finance. The technological challenges involved in building these computers are daunting, since they require precise control of light and matter at the smallest scales, but there has been significant investment and progress in the last few years.
Already, special-purpose quantum computers have been built that can sample from classically hard to simulate, albeit quite contrived, probability distributions. For example, a recent photonic quantum processor has been shown to efficiently sample from a distribution from which a state-of-the-art supercomputer would take many years to produce a single sample [1]. Given the power of these extant small-scale quantum computers, and the fact that larger scale “universal” quantum computers will take several more years to build, there is a lot of interest in developing useful applications for these sampling tasks.
At ORCA Computing, we are investigating applications of these near-term quantum computers for generative modelling, with implications for finance. Synthetic data plays an important role in finance, for instance for compliance purposes where data is scarce, developing testing environments, preserving privacy, or developing downstream machine learning applications. For example, to support innovation, the financial conduct authority (FCA) provides a sandbox environment with high-quality synthetic data. Whereas traditional financial time series models such as ARCH and GARCH can be used, there is growing demand for more data-driven generative models that can produce higher quality data.
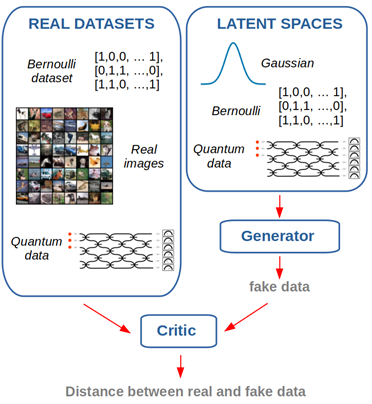
Modern generative models such as generative adversarial networks (GANs) or diffusion models rely on learning transformations between data and a high-dimensional “latent space”. For example, the generator in a GAN draws a sample from a latent distribution, which is often a high-dimensional normal distribution, and learns to map it to a datapoint that is sufficiently realistic that it can fool a discriminator (see figure above). Different data can be generated by sampling different points within the latent space. The importance of using a rich and expressive latent space has been highlighted several times in the literature: for example, Karras et al [2] report improved performance when transforming an initially uncorrelated multivariate normal latent space into a more complex and correlated latent space that facilitates the downstream generation task. Since the distributions from which near-term quantum computers can efficiently sample are particularly rich and complex, they are promising candidates for representing latent spaces within generative models.
We find that using a quantum latent space, produced with existing photonic quantum computers, can indeed lead to improved performance on some tasks. We train GANs using latent space samples drawn from such a computer and compare the result to GANs trained using classical latent spaces such as multivariate normal and multivariate Bernoulli distributions. In a first toy experiment on synthetic Bernoulli and quantum data, we find that the cumulative probabilities of the distributions learned by a GAN are influenced by the properties of the latent space: a uniform Bernoulli or Gaussian latent distribution makes it difficult for a GAN to learn a non-uniform distribution, whereas a more concentrated quantum latent space makes it easier. When the data has some statistical properties in common with the quantum latent space, we also find that the GAN yields better results.
We also perform an experiment where the latent space is provided by a real large-scale photonic quantum processor, and the GAN is trained to generate real-world images from the CIFAR 10 dataset. This is to our knowledge the first demonstration of a generative modelling task using a quantum device in the “quantum advantage” regime that is too large to simulate even by a supercomputer. We find that using a quantum latent space produces better results, measured in terms of inception score, than the standard choice of a multivariate normal distribution. We also find that other non-standard classical latent spaces also outperform the multivariate normal distribution. This shows that large-scale generative models can benefit from using more complex latent spaces, and in particular those generated by quantum devices.
Our work demonstrates that generative models that use quantum latent spaces do exhibit different statistical properties than those that use classical latent spaces. Moreover, our approach can be scaled to large-scale data and quantum processors in the quantum advantage regime, achieving better performance than commonly used distributions.
We anticipate that the development of more expressive hybrid quantum/classical generative models can benefit financial companies by improving the quality of their synthetic data. Our future work will focus on better understanding and benchmarking the differences that can arise due to the use of a quantum latent space in large-scale data.
References:
[1] Madsen, Lars S., et al. "Quantum computational advantage with a programmable photonic processor." Nature 606.7912 (2022): 75-81.
[2] Karras, Tero, Samuli Laine, and Timo Aila. "A style-based generator architecture for generative adversarial networks." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.
William Clements is Head of Machine Learning at ORCA Computing. Join him at this years QuantMinds International where he will be presenting a case study on quantum machine learning with near-term quantum computing on Monday 7 November at 16:30.
